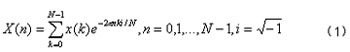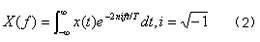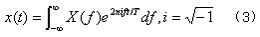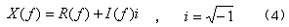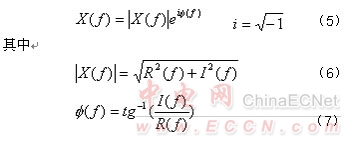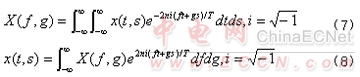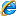傅立叶集

傅立叶是法国数学家、物理学家,傅立叶级数（三角级数）创始人。1768年3月21日生于欧塞尔， 1830年5月16日卒于巴黎。9岁父母双亡， 被当地教堂收养。12岁由一主教送入地方军事学校读书。17岁（1785）回乡教数学，1794到巴 黎，成为高等师范学校的首批学员， 次年到巴黎综合工科学校执教。1798年随拿破仑远征埃及时任军中文书和埃及研究院秘书，1801年回国后任伊泽尔 省地方长官。1817年当选为科学院院 士，1822年任该院终身秘书，后又任法兰西学院终身秘书和理工科大学校务委员会主席。

主要 贡献是在研究热的传播时创立了一套数学理论。1807年向巴黎科学院呈交《热的传播》论文， 推导 出着名的热传导方程 ，并在求解该方程时发现解函数可以由三角函数构成的级数形式表示，从而提出任一函数都可以展成三角函数的无穷级数。

1822 年在代表作《热的分析理论》中解 决了热在非均匀加热的 固体中分布传播问题，成为分析学在物理中应用的最早例证之一，对19 世纪数学和理论物理学的发展产生深远影响。傅立叶级数（即三角级数）、傅立叶分析等理论 均由此创始。其他贡献有：最早使用定积分符号，改进了代数方 程符号法则的证法和实根个数 的判别法等。

傅里叶变换能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅里叶变换具有多种不同的变体形式，如连续傅里叶变换和离散傅里叶变换.

傅里叶变换属于谐波分析。 而傅里叶变换的逆变换容易求出,而且形式与正变换非常类似;

正弦基函数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解.在线性时不变的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取.

将时域变为频域的变换，称之为傅立叶正变换；而将频域变为时域的变换，称之为傅立叶逆变换。傅立叶分析提供了获取频域信息的一种较为完整的方法，它使我们利用频率、幅值和相位来描述时域中的振动波形。

因此,傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用（例如在信号处理中，傅里叶变换的典型用途是将信号分解成幅值分量和频率分量）。

下面简单介绍快速傅立叶变换问题

在数值电路的传输中，为了避免信号干扰，需要把一个连续信号 x(t)先通过取样离散化为一列数值脉冲信号x(0), x(1), …… ,然后再通过编码送到传输电路中。如果取样间隔很小，而连续信号的时间段又很长，则所得到的数值脉冲序列将非常庞大。因此，传输这个编码信号就需要长时间的占用传输电路，相应地也需要付出昂贵的电路费用。

那么能否经过适当处理是使上述的数值脉冲序列变短，而同时又不会丧失有用的信息？的经过研究，人们发现，如果对上述数值脉冲序列作如下的变换处理：

 

 

则所得到的新序列X(0), X(1) , ……将非常有序，其值比较大的点往往集中在某一很狭窄的序列段内，这将非常有利于编码和存储，从而达到压缩信息的目的。

公式（1）就是所谓的离散傅立叶变换，简称DFT。现在我们来分析一下计算DFT所需要的工作量。如果我们不考虑公式（7.1）中指数项的运算，那么计算其每一个点X (n) 需要N次复数乘法和N-1次的复数加法。显然当N很大时，这个工作量也非常巨大。正是由于这个原因，使得DFT的应用范围在过去很长的时间里受到了严格的限制。

注意到公式（1）是非常有规律性的，那么能否利用这种规律性来降低DFT的计算时间？

1965年，凯莱和塔柯的提出了一种用于计算DFT的数学方法，大大减少了DFT的计算时间，同时又特别适用于硬件处理，这就是所谓的快速傅里叶变换，简称FFT。

鉴于DFT的数据结构可以通过傅立叶变换的离散化获得，亦可通过三角插值得到，而本质上又同连续傅里叶分析有着极为密切的关系，因此，本部分将从傅立叶级数级数和傅立叶积分入手，通过离散导出DFT结构的来源，接着分析FFT的工作原理。

如果x(t)是定义在整个实轴上的实值或复值函数，则其傅立叶变换可由下式给出：

 

 

若对任意参数f，上述积分都存在，则（2）式子确定了一个函数X(f)，称为x(t) 的傅立叶变换。如果已知X(f) 则利用如下的傅立叶逆变换，还可复原x(t) ：

 

 

若x(t) 和 X(f) 同时满足（2）、（3）式，则称他们是一个傅立叶变换对，记为 。。通常X(f) 是一个复函数，因此可以写成如下两部分：

 

式子中R(f) ，I(f) 分别是X(f) 的实部和虚部。将上式表示为指数形式：

 

 

 

工程技术中，常将x(t) 看成一时间信号，相应的空间，称为时间域和空域；将其傅立叶变换X(f) 看成频率函数，相应的空间称为频域。|X（f）| 称为x(t) 的傅立叶谱，而 称为其相角，这在物理上是有良好背景的。的譬如此频率的的含义可以这样来理解：应用欧拉公式可将指数项表示成正弦-余弦的形式，如果把（2）式解释成离散项和的极限，则显然X(f)是包含了无限项正弦-余弦的和，而且f 的每一个值确定了所对应的正弦-余弦的频率。

在以后的叙述中，我们不妨用t表示时间，用f表示频率；同时用小写字母表示时间函数，并用相应的大写字母表示其傅立叶变换。

傅立叶变换可很容易地推广到二维情形。假设x(t , s)是连续的和可积的，且X(f , g)是可积的，则相应的傅立叶变换对如下：